Work in progress

I’ll try to give a summary over the components of Delf and Delg

Paper

DELF:

DELG:

GeM:

ArcFace:

Delg

In Delg we use local and global features. The local features are build from the shallow part of the CNN, for example we use the output of conv4 from ResNet50 and the output of conv5 for the deeper global features.

Local features

Let \(\chi_k\) be the set of \(W \times H\) activations for feature map \(k \in{\{1...K\}}\) . Each point on a feature map has a receptive field on the original image and if its pixel is activated, its indicating the presence of that feature in that receptive field. We use all channels from a pixel on a feature map as a local descriptor/feature.

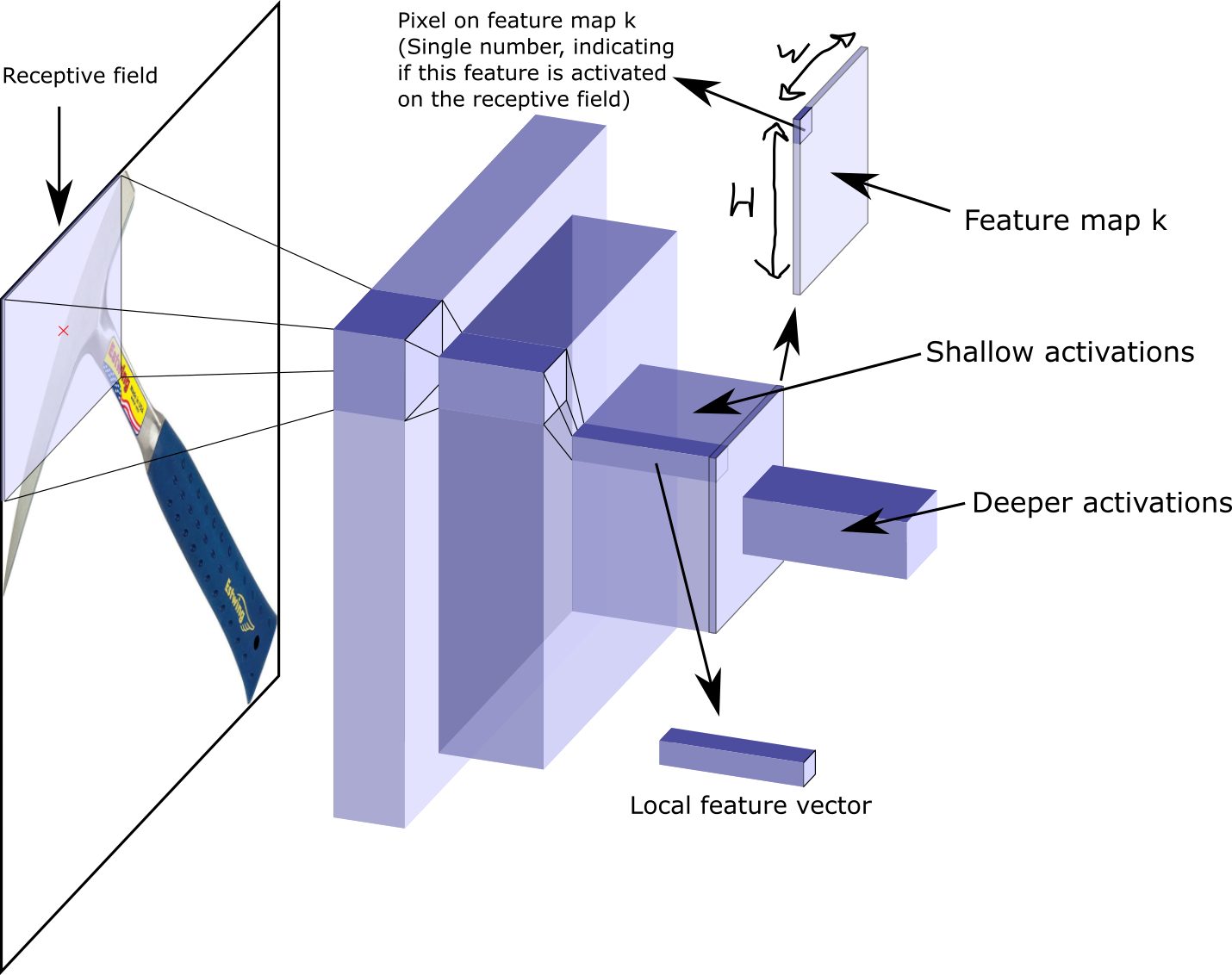
To reduce the size of the local feature vector, an autoencoder gets employed in Delg. At the end the vector gets l2-normalized.

l2-normalization

What does it mean to l2-regularize here?

Global feature

For the global feature vector we employ Generalized-Mean (GeM) pooling on the deeper output of the CNN with the aim to reduce each feature map to one single number (global pooling). To understand this ill quickly remind you of the pooling methods.

Global Max Pooling

There is global max pooling (MAC) given by: \begin{equation} f^{m}=[f_1^{m} … f_k^{m} .. f_K^{m}]^T, f_k^{m} = \max_{x \in \chi_k} x \end{equation} Max pooling on a feature map results in a number, indicating how present the feature is anywhere on the featuremap. If you keep the location of the max you can tell where the feature is present on the image by the receptive field. We implicitly compare one image patch.

Global Mean Pooling

There is average pooling (SPoC) given by: \begin{equation} f^{a} = [ f_1^{a} … f_k^{a} … f_K^{a}]^T, f_k^{a}= \frac{1}{|\chi_k|} \sum_{x \in \chi_k} x \end{equation} Mean pooling describes how often and how strong a feature is present in the image overall.

Generalized-Mean Pooling

GeM pooling is a parametrized mixture of max and average pooling and given by: \begin{equation} f^{g}=[f_1^{g}…f_k^{g}…f_K^{g}]^T, f_k^{g} = ( \frac{1}{|\chi_k|} \sum_{x \in \chi_k} x^{p_k})^{ \frac{1}{p_k}} \end{equation} where the pooling parameter \(p_k\) can be manually set or learned. A large \(p\) would amplify single entries and the operation would resemble max pooling.
GeM pooling shows better results then mean or max pooling.

One last question i had, what if we use mean and max pooling and let a fc decide how to use it? -> No exponentiation, could be faster and the CNN could optimize it…

Whitening of the aggregated representation vector

Basically PCA + normalize the PCA Data. Results in that all dimensions get equal contributions. Noise gets attenuated! Whitening is only done on the train set! The validation data gets preprocessed with the from training inferred parameters. whitening downweights co-occurences of local features, which isgenerally beneficial for retrieval applications here

Arcface margin

Intra-class

variation of objects in the same class

Inter-class

variation between objects of different classes

Softmax-cross-entropy loss does not optimize for high intra-class similarity of the feature vector and it does not optimize for diversity for inter-class samples. We want something that puts together objects of the same class and put a large boundary between objects of different classes. ArcFace helps, it is easy to implement, has low computational overhad and good convergence properties.

Consider the last two layers \(i\) and \(j\) of the CNN (Dense layers). Layer \(i\) has \(d = 512\) outputs, subsequent layer \(j\) has \(n\) output units. So we have \(W \in R^{d \times n}\) weights to compute the output of the last layer. \(x_i\) is the output of the first layer. Instead of directly computing the logits as \(W_j^T x_i\) we use the formula \begin{equation} W_j^T x_i = |W_j| |x_i| \cos{\theta_j} \end{equation} from which we want to get \(\theta\). So we need to caluclate \(\frac{W_j}{|W_j|}\), \(\frac{x_i}{|x_i|}\) and take the \(\arccos\) to get \(\theta\).
The parameter of the ArcFace, the additative margin penalty \(m\) gets added to \(\theta\). The higher theta… todo

Here we add the additative margin penalty \(m\). There are also SphereFace which multiplacative angular margin and CosFace with additive cosine margin. Ganz hab ich noch nicht verstanden. Man nutzt arcface nur wenn in bestimmten winkeln.

from the last layer in the network, we normalize the weights and the feature beforehand

Softplus activation

Softplus is always positive and ranges from 0 to infinity. Its a smooth function and its differntiable at x = 0. ReLU is more efficient to calculate

Receptive fields

I recommend reading this.

Q&A

What is the required input size for images?

• You have to distinguish between training and inference. The Model is build fully convolutional and can handle arbitrary input sizes. But for training we have to apply dense layers which define the input size. At inference time we construct an image pyramid, extract features for each size and then select a subset or all features. In Delf we trained the attention network seperately, delg has unified it. But i guess, the aspect ratio augmentation is now very important?